It is a multivariate generalization of the beta distribution. A $k$ -dimensional Dirichlet random variable $x$ can take values in the $(k − 1)$ -simplex (a $k$ -vector $x$ lies in the $(k − 1)$ -simplex if $x_i \geq 0$ , $\sum_{i=1}^k x_i = 1$ ).

PDF:

f (x 1, \dots, x K; α 1, \dots, α K) = 1 B ( α ) \prod i = 1 K x α i - 1 i

$f\left(x_{1},\cdots ,x_{K};\alpha _{1},\cdots ,\alpha _{K}\right)={\frac {1}{\mathrm {B} ({\boldsymbol {\alpha }})}}\prod _{i=1}^{K}x_{i}^{\alpha _{i}-1}$

where the parameter $\boldsymbol\alpha$ is a $k$ -vector with components $\alpha_i > 0$ and the multivariate Beta function acts as the normalizing constant:

B (α) = \prod K i = 1 Γ ( α i ) Γ ( \sum K i = 1 α i )

$\mathrm {B} ({\boldsymbol {\alpha }})={\frac {\prod _{i=1}^{K}\Gamma (\alpha _{i})}{\Gamma \left(\sum _{i=1}^{K}\alpha _{i}\right)}}$

It's the conjugate prior of the multinomial distribution.

Properties:

E (x i) = α i \sum K k = 1 α k

$\operatorname{E}(x_i)=\frac{\alpha_i}{\sum_{k=1}^K \alpha_k}$

Var (x i) = α i ( \sum K k = 1 α k - α i ) ( \sum K k = 1 α k ) 2 ( \sum K k = 1 α k + 1 )

$\operatorname{Var}(x_i)= \frac{\alpha_i\left(\sum_{k=1}^K \alpha_k-\alpha_i\right)} {\left(\sum_{k=1}^K \alpha_k\right)^2\left(\sum_{k=1}^K \alpha_k+1\right)}$

In symmetric Dirichlet distribution (where all of the elements making up the parameter vector 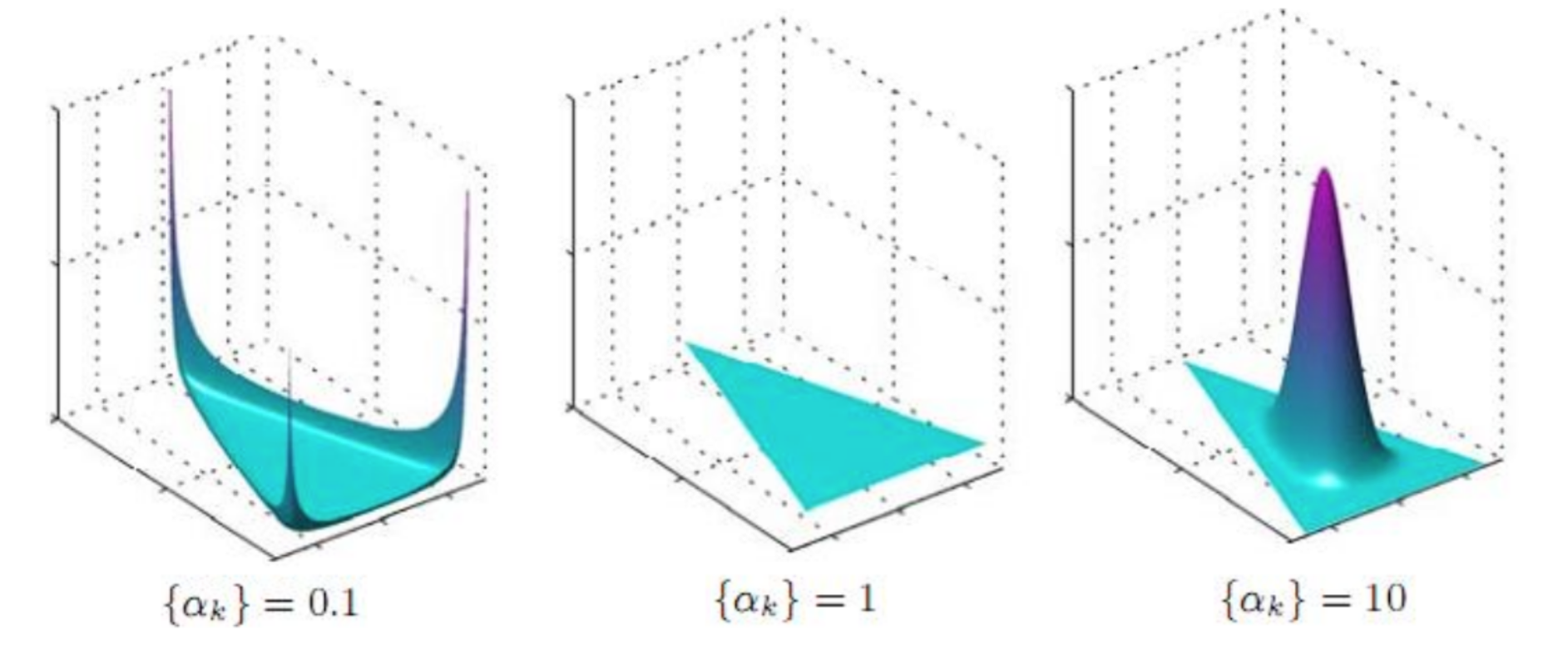${\boldsymbol {\alpha }}$ have the same value):

General examples: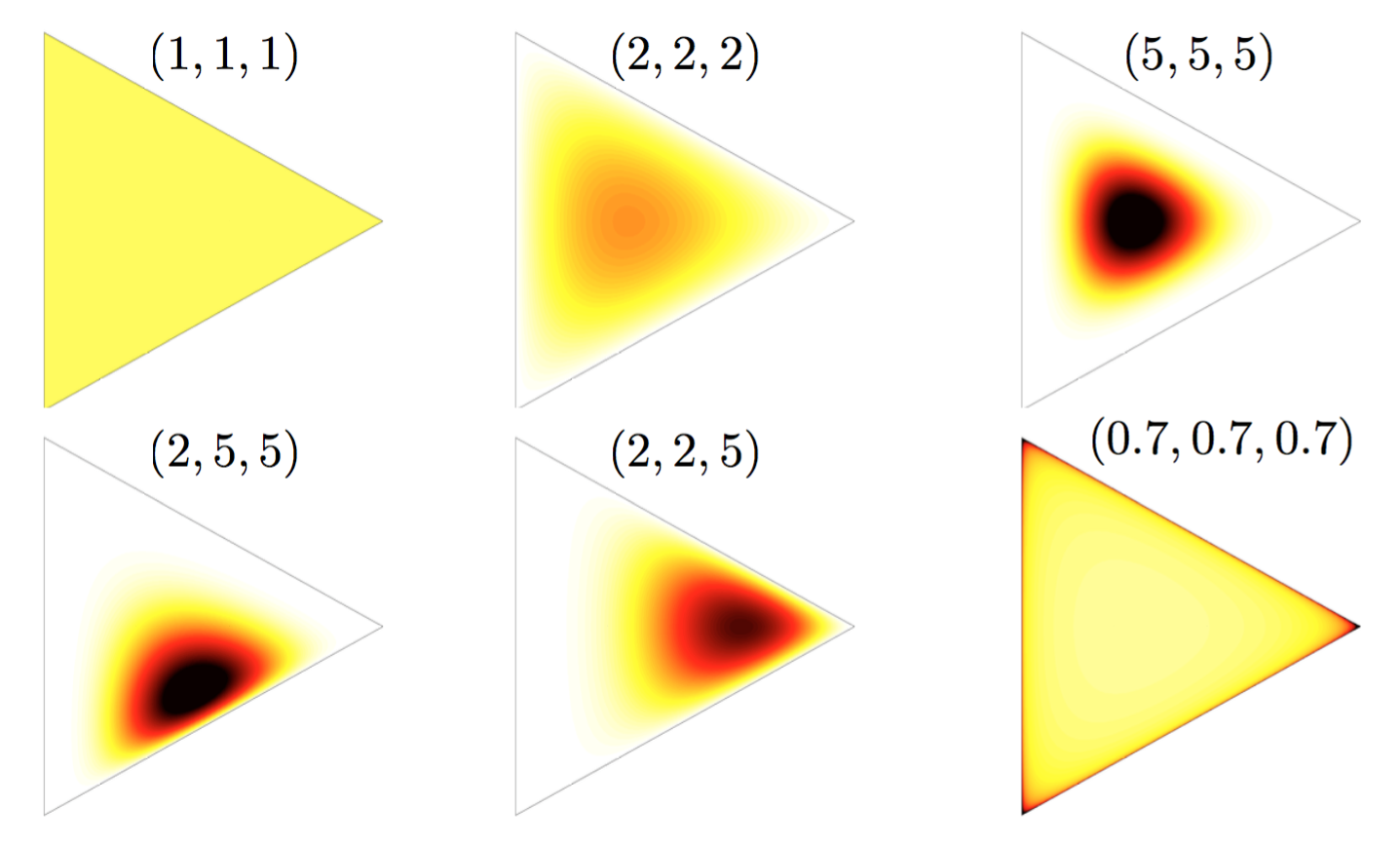
QQ20160905-0@2x.png

Reference

Dirichlet distribution: https://en.wikipedia.org/wiki/Dirichlet_distribution
Nonparametric Baysian Models: http://videolectures.net/mlss09uk_teh_nbm/
Blei, David M., Andrew Y. Ng, and Michael I. Jordan. "Latent dirichlet allocation." Journal of machine Learning research 3.Jan (2003): 993-1022.

Dirichlet Distribution

Reference